- 其实比赛已经结束很久了,一直没空写(更准确说,懒得写),今天开始,花几天写一下。
题目描述
RoadsAndJunctions 原问题连接
大致题意
二维平面上有$NC$个城市,你需要建一个公路系统将所有城市连通起来。构建这个系统有两种操作:
- 1 在地图上某个没有东西的位置上,修建一个中转站,修建花费$junctionCost$的费用
- 2 在两个城市间 or 两个中转站间 or 一个城市一个中转站间,建一条路(直线段),花费$length_{road}$的费用(即$1$单位长的路花$1$的费用)
但是整个过程分以下几步完成:
- 首先,你先决定哪些位置建造中转站,最多可以选$2 * NC$个地址建中转站,一次性把所有选址确定下来,发给判题程序;
- 然后,该程序会以$prob_{failed}$的几率独立判定每个选址的中转站是否建造失败,然后将所有建造成功的中转站告诉你;
- 之后,你需要修若干条路,将这些中转站与城市全部连通起来。
- 总花费就是你的得分,越低越好。(不论中转站建造是不是成功,只要选址了,就产生花费。)
历程回顾
这是今年TCO马拉松的资格赛第一场,所以还算比较重视,毕竟进了Top50才能获得积分。
由于,工作日加班比较多,很难有功夫写点代码,所以在周末前基本处于心算模式。关于心算模式,今年才有了一些心得。过去业余时间相对更多些,更喜欢花大部分的时间 写逻辑+做优化,信奉更多的尝试会有很多的机会,其实结果大多并不好。现在时间少了,人也懒了,反倒更愿意花更多的时间去规划思路、翻看论文、构建debug(可视化)环境 这类琐事上,对于写逻辑更追求一击必中,优化也是花更多的时间找到问题所在,才迟迟下手。其实,后来发现这个策略往往更节约精力,也能清楚的明白每一步提升的来源,当然成绩也会更加稳定。
这个问题,相比于波兰特别场,我其实吃了点见识少的亏。这个问题的原型其实是一个金典问题——Steiner Tree(斯坦纳树),而我之前并不知道这个玩意,所以一些“显然”的性质被忽视掉了,导致在有限的时间内算法无法完成更多的迭代致使最后的效果不是那么好,最终卡在了69名,没能进Top50,也就没有积分啦。不过还好,还有3场,还有机会拿积分的。
不过,这场也有些趣事发生,比赛过程看似风平浪静,但结束后开始判分时,Psyho直接对这个题目的随机设置与评价方法开炮,引发了论坛激烈的讨论。作为吃瓜群众,自然强势围观。
论坛争论的焦点在于测试集是否足够大 or 有效,可以区分出大家的算法的优劣?毕竟是淘汰赛,这个问题是否有选拔意义。观点大致3派:
- 这题出的太没技术含量派,主要观点: 我就是为了吐槽这题而来吐槽这题的。这派觉得这个问题随机性太强,不适合作为选拔赛的问题。
- 这题应该修改判题策略派,主要观点: 加数据量,或增加每个数据的随机次数,以消除随机对排名的影响。
- 这题应该按原始规则进行派,主要观点: 保持原始的规则,因为比赛已经结束了,规则不应该在结束的时候改。更何况很多人在one-hit方面做了优化,改规则对他们不利。
至于我的观点,我更倾向于第3派。第2派虽然有道理,但却造成了不公平(尤其像我这种被某苏省高考隔三差五改革坑出翔的偏科选手,对这种没事该规则的玩法表示没法支持);对于第1派,只能说你说的很有道理,但是一切都结束了,才说这些牢骚也没啥实质的意义,当然吐槽一下也没啥不对就是了。
这个问题的随机到底有多厉害呢?在跑正式数据前,我排97左右,跑完正式数据我就提升到69了。是不是很随机?
感慨,大佬们居然还有精力花在one-hit的策略探索上.....这帮老外都不用加班的么?
个人思路简介
我的思路相对比较简单。
首先,看第二部分,因为城市与中转站已经不能再修改,显然这就是是个最小生成树问题。因为不可能成为主要的得分点,所以就不多述了。
主要看第一部分的求解。
虽然,比赛期间并不知道斯坦纳树,但幸运的是我知道三角形的费马点,这是个非常重要的点(虽然也许你也能在比赛中发现这个东西,但是直接知道会节约很多乱思考的时间)。费马点大致如下图:
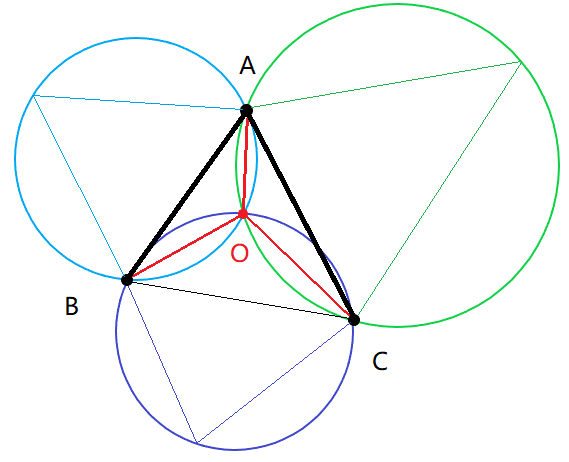
其中,O点就是费马点。它是三角形ABC分别向外做等边三角形的外接圆的焦点。它的特性是到$L{OA}+L{OB}+L{OC}$取到最小值(即到三点距离和最小)。当然,往往也存在$L{OA} + L{OB} + L{OC} < L{AB} + L{AC}$。即在生成树里,可以通过添加这个点,来减小生成树的权重。恰好,这也是Steiner Tree求解中比较重要的方法之一。
我的思路比较简单,大致如下:
第一部分:
- 对每个点,枚举其周围不远处的点所构成的三角形,依次求解其费马点,并存入种子库$SeedSet$中;
- 将所有的种子库中费马点与所有的城市放在一起,求一次最小生成树,并将这些费马点中,可以不通过城市就连通的点集组成一个个的集块;
- 分别测试每个集块里的飞马点,方案:随机加入一个费马点,通过模特卡罗模拟测试加入后是否能更优,用退火的方式调整这些点的位置,测试能否更优,从而确定每个集块加入哪些点;
- 将所有集块合并起来,再蒙特卡洛求期望;
- 尝试随机删除,并移动一些点,蒙特卡洛测试是否能更优;
因为用到了蒙特卡洛方法,可以想象其效率值感人,显然不能担当大任,最初非常耗时,几乎10s中就做不了几次测试。不过做了以下优化:
- 剪边。最终在最小生成树中城市与城市之间的边,一定在只有城市的条件下最小生成树的边集里。所以N个城市只用存N-1条边即可。同样这个思想可以用在减少中转站的连边的问题上。
- 移动中转站坐标时,不改变最小生成树的连接情况,即点A连着点B,那么移动A后,默认树中A还是连着B,而不再重新求解一遍最小生成树。这个只是为了找局部最优。当然,这个简化也失去了求解全局最优的能力。
- 直接在蒙特卡洛已生成的最小生成树集合上模拟,就不用再求蒙特卡洛了。
这样能把效率平均提高几千倍吧。不过好像对成绩提高,实在有限。
第二部分:
- 这里会在第一部分生成的点集基础上,随机加入、删除、移动节点,来试图找到更优的解。纯看脸。
- 对于添加节点,我试图在已有的点旁边直接加一个点,这个其实很有效,确保了某个中转站有更大的概率能建成。
- 为了稳定性,因为成绩实在太随机了,最后一次提交将蒙特卡洛的模拟次数加到了200,当然这也意味着牺牲了更多的尝试机会。
最后的成绩:
只能说一般般了。
实际上,可以不需要蒙特卡洛的
这是在赛后看大家的讨论中,发现了Steiner Tree的存在,才恍然意识到不用蒙特卡洛也是可以的。
先说说欧式二维空间Steiner Tree的两个特殊性质:
- 添加的节点不多于$N-2$个
- 每个添加的节点在树中,度永远是$3$,且连边的夹角是120度
很显然,能得出以下优化:
- 度小于等于$2$的节点,没必要添加;
- 大部分添加节点相互间是独立的,因为它们一定在某个三角形内,所以它的影响作用域只有3个节点。所以评估一个节点好坏时,只需要关心它与周围这几个节点即可,而不需要求解所有节点的最小生成树;
如果加入这两条,前面的效率会大大提升,也就添加了更多的可能。同时,我们也不需要完全依赖盲目的随机,可以在寻找中间节点时,增加更多的启发式。
关于蒙特卡洛
这玩意可能中学就会接触到。但真正觉得神奇大概也是在接触了蒙特卡洛树搜索(MCTS)后,才会觉得神奇。其实,最早这个方案就是评估类似围棋这类游戏的状态好坏的,只是AlphaGo加入了深度神经网络使其更加强悍罢了。
蒙特卡洛方法似乎是一种不需要知识就能工作的通用方法,但这也给了人们我们找到了万能、无敌方法的假象。这其实是一个很危险的思想,因为以目前的技术来看,算力还远远没有达到可以任意挥霍的水平。所以个人觉得这种方法更多时候还是找找灵感的玩具吧。有些实在没有进展的领域,用其临时填补技术空白,也未尝不可。
one hit
这玩意,一般是不需要用的,因为,通常在大数据(极多次数模型)的条件下,结果会收敛在期望值上。不过这个问题不同,对于许多case,其方差及其恐怖,而最终测试用例也只有区区2000,因此有必要采用这个策略。
这个策略的idea也很简单:合理的保守。实现的话,各凭本事咯。不过,我觉得还是可以有个基本框架的,比如:
- 比如基于$Pro$的概率不低于$Score*$的假设,直接设定一个case的价值为$Score*$。(很显然,用期望作为评估,$Pro=0.50$。)只要$Pro$更大,你就能获得更保守的策略
- 当然,类正态分布,可以用$F(X) = Exp(X) - \alpha * \delta(X)$作为评价函数。
大佬们的策略
突然发现已经有大佬写了一个总结,嗯,感觉很不错的样子。
贴个链接
不早了,睡了。